Evaluate the principal stresses and principal planes:

The state of stress at a point in a loaded solid is given on two faces of an element whose shape is a triangular prism as illustrated in Figure. Evaluate the principal stresses & principal planes.

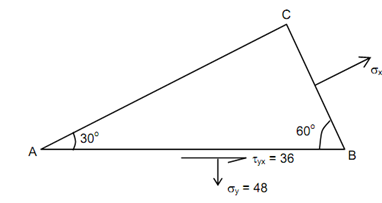
Figure

Solution

Here, we ought to first get the value of s_x and subsequent calculations shall be a standard set.

Given  s_y = 48 MP_a

t_yx = 36 MP_a    ∴          t_xy = - 36 MPa

s ₃₀ ^o = 60 MP_a (aspect angle of plane BC is + 30^o)

s₃₀^o  =( s_x+ s_y ) /2 + ((s_x -  s_y) /2 ) cos (2´30^o)  + t_xy sin (2´30^o)

60  =( s_x+ 48) /2 + ((s_x -  48) /2 ) cos (60^o)  + (-36) sin 60^o

60 = s_x /2  + 24 + (s_x /2 ) cos 60^o    -  24 cos 60^o  -36 sin 60^o

i.e. 60  = (s_x /2 )(1+ cos 60^o)    + 24- 24 cos 60^o  -36 sin 60^o

∴ s_x = 2/ (1+0.5)[60-24-(-24´0.5)-(-36)´0.866]

     =2/1.5 [79.177]=105.57MPa

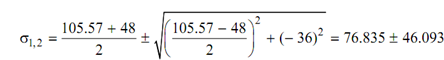
s ₁ =76.835 + 46.093MP_a

 s ₂ =76.835 - 46.093MP_a

Assume the aspect angles of the principal planes be f

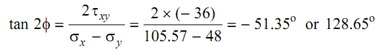
f = -25.6715 or or 64.325⁰

Substituting

f= - 25.675^o  (or 2f = - 51.35^o ) in expression for s_n

s_n  =( 105.57 + 48 )/2 +( 105.57 - 48)/2 cos (- 51.35^o ) - 36 sin (- 51.35^o )

= 122.92 MPa

f₁  = - 25.675o  and f₂  = 64.325^o