Determine the maximum value of the shear stress:

A machine component is built of a material whose final strength in tension; compression and shear are 40 N/mm², 110 N/mm² & 55 N/mm² respectively. At the critical pt within the component the state of stress is shows by

σ_x = 25 kN/mm² and σ_y = -75 kN/mm².

Determine the maximum value of the shear stress t_xy which shall cause failure of the component and also define the mode of failure.

Solution

Given state of stress :  σ_x = 25 kN/mm²

σ_y = -75 kN/mm².

We have to discover what t_xy is safe, if σ₁ ≤ 40 kN/mm², σ₂ ≥ -110 kN/mm² and

t_max ? 55 kN/mm².

The above three conditions are to be satisfied independently.

Now,

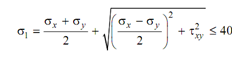
In the limiting case,

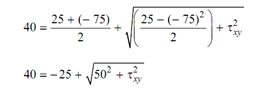
or         t²_xy = [ 40 - (-25) ]²  - 50² = 1725

            ∴          t_xy  = ± 41.533 N/mm²

Note down that the limiting case of σ₁ = 40 N/mm² will take place for both the t_xy values of 41.533 N/mm² and - 41.533 N/mm². But the planes of failure shall be different.

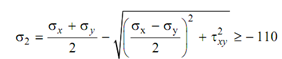
In the limiting case,

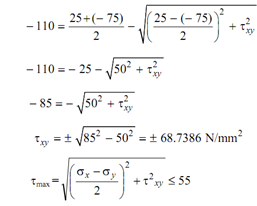
i.e.       50² + t²_xy  = (55)²

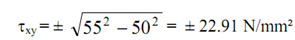
The permissible value of t_xy is different for different limiting criteria, that is

| txy | ≤ 41.53 if σ₁  ≤ 40

≤ 68.74 if σ₂  ≥ - 110

≤ 22.91 if t_max  ?  55

Therefore, we find that the maximum safe value of t_xy is just 22.91 N/mm² and the material shall fail in shearing mode.