Calculation of Principal Planes and Principal Stresses:

Equating ds_n / dq  to zero, we obtain

txy cos 2q + (s _y - s_x /2) sin 2q= 0

or         sin 2q / cos 2q =  - 2t _xy / ( (s _y - s _x )/2) =  2t _xy /  ((s_x - s _y )/2)   ------------(1)

Mentioning the specific angles defining principal planes by f₁ and f₂,

or         tan 2f =2t xy / (s _x - s _y)           ----------- (2)

Eq. (1) gives a condition for the determination of principal planes. Eq. (1) shall have two solutions in the range -π/2 < f < π/2 and they shall give the orientation of principal planes.

Further, the second derivatives,d²s_n /dq² , shall be negative for the solution f₁ (aspect angle of the major principal plane) and positive for the solution f₂ (aspect angle of the minor principal plane). Let us attain these expressions too.

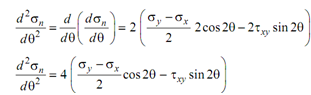
After attuning the solutions f1 and f2 of Eq. (1), their values might be substituted in the

expression for d ²s_n/dq² given in Eq. (2) and the major & minor principal planes might be identified. But in practical solutions this step is hardly ever required. Instead of, put the two solutions f₁ and f₂ in the expression for normal stress and get the values of principal stresses σ₁ and σ₂ and corresponding principal planes might be identified.

Now, let us derive the common expressions for the principal stresses. As, we know that

 tan 2f = 2t xy / (s _x - s _y) on a principal plane, we might write as

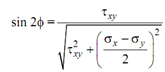             ----------- (3)

and

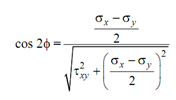      -------------- (4)

 putting Eqs. (3) and (4) in the expression for σ_n, we get

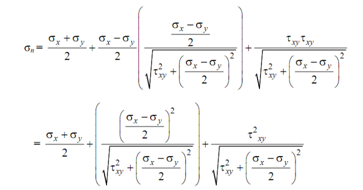
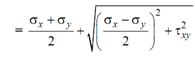
Since  shall have two roots namely 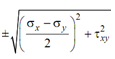 , we might write the ultimate expression for major & minor principal stresses as follows:

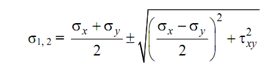       ----------- (5)

Eqs. (1) and (5) might be utilized to readily determine the principal planes and principal stresses.

Let us now have an instance for determination of principal stress & principal planes, specified the state of stress.