Liquid Pressure at a Point:

Equivalently, we can say that the pressure at point A is equal to the weight of the liquid in a column of unit cross-sectional area and height h (vertical distance of the point A from the free surface of liquid). Thus, we can write:

 P = h ρ g.

 Eq. implies that the pressure of fluid is proportional to the height of the column: as the height of the liquid column (or the depth of the point under consideration) increases, the pressure raise. Also note that the fluid pressure does not depend upon the total mass or total volume of the liquid.

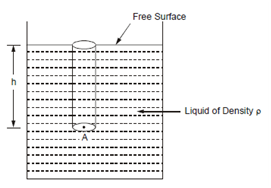
Figure: Liquid Pressure at a Point A inside the Liquid

The pressure-depth relation of a fluid can be demonstrated using an apparatus shown in Figure 6. It consists of a cylindrical container in which there are small holes on the surface along a line parallel to its axis. Keeping all the holes closed, the container is filled with water and put on a flat surface. When all the holes are opened simultaneously, that is observed in which the water jets coming out from different holes touches the surface at different distances from the axis of the container : the jet from the lowest hole falls farthest and that from the top most one falls closest to the base. This clearly display that the pressure exerted by the liquid near the lower hole is highest and vice-versa.

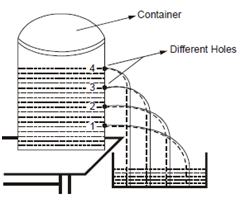
Figure: Pressure of Liquid Coming out from Different Holes Depends on their Depth from the Free Surface of the Liquid