Relaxation Time

Each system reacts in another way whenever changes in its properties are forced by some exterior agency. For illustration, consider a system for which the equation z = f (x, y) is the equation of state that associates the equilibrium values of the properties x, y and z. When this system is rapidly subjected to change Δx in x, with y kept constant, z ultimately reaches the new value predicted by the equation of state, viz.

                               z + Δz = f (x + Δx, y)

The key word in the final sentence is ultimately. The change Δz takes time. A definite time T passes before equilibrium is restored to the extent that no further modifications in the properties are measurable anywhere in the system. T is termed as the relaxation time. The procedure by which a system resumes equilibrium after a rapid change in one of its properties is termed as the relaxation process.

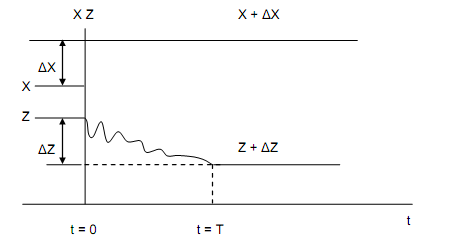
                                               Figure: Illustration of the definition of Relaxation Time

The figure above illustrates the definition of T. There are many systems that approach equilibrium at the similar rate as the function exp (-t/T_e) approaches to zero. In most situations T and T_e are of similar order of magnitude.

In common, the relaxation time T is a complex function of all the properties of the system, of the magnitude of the impressed change Δx, and of the position where Δx is impressed. In some situations T might be computed from appropriate mathematical models, though in most situations it is a measured quantity.

The science of gas dynamics gives numerous illustrations of relaxation processes in gas systems subjected to step changes in pressure, temperature, and volume. For the reason of thermodynamics it is only essential to know that limited time, termed as the relaxation time, passes before a system returns to equilibrium after a rapid change in any of its properties.