Find the corrected bearing of the lines:

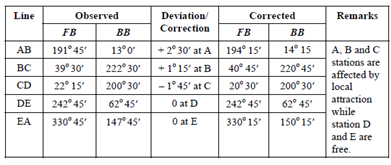
Measurements of bearings, while running a traverse ABCDE are recorded in table given below.

It is suspected that reading at some survey stations were effected by local attraction. Locate the stations affected by local attraction and find the corrected bearing of the lines.

Solution

The first step is to obtain the difference between FB and BB of every line and obtain its deviation from 180^o.

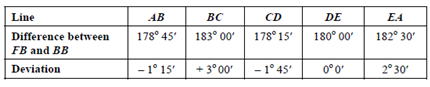
It is thus found that line DE has a perfect difference of 180^o between fore bearing and back bearing. It can be concluded that station D and station E are free from local attraction.

Observed fore bearing EA and back bearing CD, are assumed to be correct. Since deviation at A is + 2^o 30′. The needle is deflecting to an amount of 2^o 30′ from true north towards east.

Correction to all readings of bearing taken at station A, therefore, shall be + 2^o 30′, i.e. fore bearing of AB at A is corrected to 191^o 45′ + 2^o 30′ = 194^o 15′ and the back bearing of line EA at A = 147^o 45′ + 2^o 30′ = 150^o 15′.

The corrected back bearing of line AB would be = Corrected FB of AB at

A - 180^o = 194^o 15′ - 180^o = 14^o 15′.

However, the observed back bearing of line AB at station B is 13^o. This indicates that station B is also affected by local attraction needle deflecting east wards by an amount 1o15′ from true north. (14^o 5′ - 13^o = + 1^o15′)

Bearings at B are required to be corrected by + 1^o15′.

Hence the fore bearing of BC as corrected would be

39^o 30′ + 1^o 15′ = 40^o 45′.

The corrected back bearing of BC at C would be 40^o 45′ +180^o = 220^o 45′. The observed back bearing of line BC at C is however 222^o 30′. This concludes that needle at C is deflected (220^o 45′ - 222^o 30′) = - 1^o 45′ from true north. Negative sign indicting deflection towards west.

The corrected fore bearing of line CD would be 22^o 15′ - 1^o 45′ = 20^o 30′

Corrected back bearing at CD at station D would be

20^o 30 ′ + 180^o = 200^o 30′.

The observed back bearing of DC at D = 200^o 30′ giving a zero deviation at D indicating station D is free from local attraction.  Similarly station E will also be free from local attraction.

The results can be tabulated as follows :