Find out the angle:

Find out the angle among lines OA and OB in following cases where the respective bearings are:

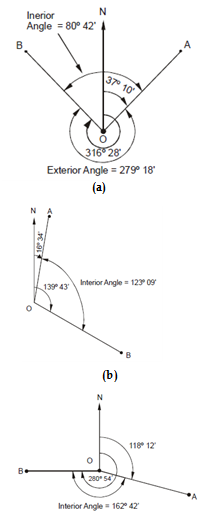
(a)        37^o 10′ and 316^o 28′ (b)          16^o 34′ and 139^o 43′ (c)          118^o 12′ and 287^o 54′

Solution

[Rule:  When bearing of two lines as measured from point of intersection of lines, i.e. from O, and lines OA and OB are given, subtract smaller from greater. The difference that will be interior angle if it is less than 180o and exterior angle if it is more. Interior angle will then be (360^o - exterior angle).]

(a)        OA = 37^o 10′, OB = 316^o 28′

Included angle = 316^o 28′ - 37^o 10′

= 279^o 18′ > 180^o ⇒ Exterior angle

Interior angle AOB = 360^o - 279^o 18′

= 80^o 42′

(b)       OA = 16o 34′, OB = 139^o 43′

Included angle = 139^o 43′ - 16^o 34′

= 123^o 09′ < 180^o ⇒ Interior angle

Interior angle   = 123^o 09′

(c)        OA = 118^o 12′, OB = 280^o 54′

Included angle = 280^o 54′ - 118^o 12′

= 162^o 42′< 180^o ⇒ Interior angle. Interior angle = 162^o 42′.

(c)

Figure: Included Angles