Uniform stretching force:

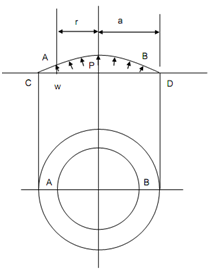
Let given Figure represent a membrane stretched over a circular hole. Uniform stretching force S and lateral pressure p act upon the membrane. A concentric part of membrane, whose radius is r is illustrated between A and B. The tensile force S, which resists the force because of pressure, p, acts along tangents from A and B. The angle among the tangent and the base line CD is dw/ dr where w is the deflection of membrane at A and B and at every point on the circle of radius r.  dw/ dr is a small angle

∴ 2π r S (dw/dr) = π r ² p

or dw/ dr =  p r/2S

Figure

Put for p / S from Eq.

dw / dr = G θ r

 You must recognise that right hand side of above equation gives the shearing stress in the cross-section of a circular bar at a radius r for unit length. Therefore, the slope of membrane at any point gives the shearing stress at the corresponding point in the section of the shaft.

The volume included in the membrane above the plane of the boundary is calculated as

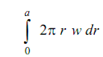
in which w is substituted from Eq. (38) that is obtained as

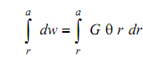
= (G θ/2 ) (a²  - r ² )

∴          Enclosed volume =

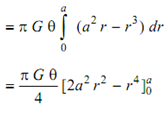
 = (π G θ /4 )a⁴

Using a = d /2

Volume, V = (G θ  /2)  . π d ⁴   /32 = (G θ/2)   J

Hence,

2V = G θ J

 The right hand side is the torque per unit length.

Therefore, twice the volume enclosed between deflected membrane and plane of the boundary is equal to the torque whereas the maximum slope of membrane at any point gives the stress. For application to practical situations we ought to visualise the deflected shape. The surface contours shall tend to run parallel to the boundaries but shall not pass through the corners showing that slope at corners is zero, so are the stresses. In more complicates section experiments method using soap film is utilized to measure slope and volume.