Velocity of Sliding:

If the surfaces of the two bodies are in contact, there may be sliding motion among them along with common tangent t - t at A.

Component of V_A1 along common tangent = V_A1 sin α

Component of V _A2 along common tangent = V_A2 sin β

Velocity of sliding = V_A1 sin α - V_A2 sin β

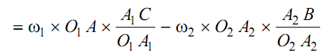
= ω₁ × A₁ C - ω₂A₂ B

 = ω₁ ( PC + A₁ P) - ω₂ ( PB - A₂ P)

= (ω₁ A₁ P + ω₂ A₂ P) + (ω₁ PC - ω₂ PB)

As, A₁ and A₂ are coincident points at A.

Thus,

A₁ P = A₂ P = AP

Therefore, velocity of sliding = AP (ω₁ + ω₂ ) + (ω₁ PC - ω₂ PB)

From alike triangles O₁ PC and O₂ PB

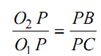
Thus, from Eq. (8.1),

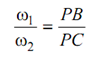
or,

ω₁ PC = ω₂ PB

or,

 ω₁ PC - ω₂ PB = 0

Velocity of sliding = AP (ω₁ + ω₂ )                          . . . (8.2)

 From Eq. (8.2), the velocity of sliding is equivalent to sum of angular velocities of two bodies multiplied by distance of point of contact through fixed point P that is called pitch point.