Law of Gearing:
The law of gearing states that the general normal at the point of contact of two bodies that are in contact, when transfering motion, must always passes by the means a fixed point known as pitch point on the line joining the centres of rotation of the two bodies.
Two bodies may be considered having general shape as illustrate in Figure. Assume point A1 on body (1) be in contact having point A2 of body (2). Points A1 & A2 are coincident points at A. Assume the common normal at point A be n - n & common tangent be t - t.
Assume ω1 be angular velocity of body (1)
ω2 be angular velocity of body (2)
VA1 be linear velocity of point A1
VA2 be linear velocity of point A2
∴ VA1 = ω1 × O1 A1 and VA2 = ω2 × O2 A2
The direction of V A1 is perpendicular to O1 A1 and the direction of V A2 is perpendicular to O2 A2. The perpendicular may be dropped on n - n from O1 & O2 that are O1 C and O2 B, respectively. Assume angle among O1 A1 & O1 C be 'α' and angle among O2 A2 & O2 B be β. Thus, V A1 & V A2 are inclined to n - n respectively by α and β, as illustrated in Figure. The components of V A1 & V A2 along common normal are respectively V A1 cos α & VA2 cos β,.
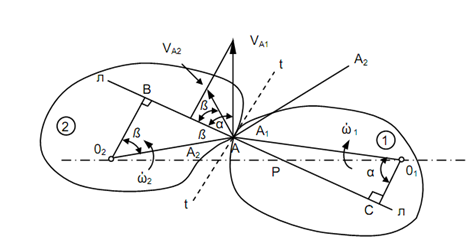
The relative velocity along n - n = V A1 cos α - V A2 cos β.
The common normal is line of transmission of motion the relative velocity with this line must be zero to avoid separation or penetration.
Thus,
VA1 cos α - VA 2cos β = 0
or,
VA1 cos α = VA2 cos β
or,
ω1 O1 A1 cos α = ω2 O2 A2 cos β
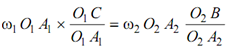
or
ω1 × O1 C = ω2 × O2 B
or,
ω1 = O2 B
ω2 = O1 C
? Δs O1 P C and O2 P B are alike.
Thus,
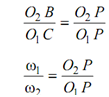 . . . (8.1)
. . . (8.1)
Therefore, if it is desired that the velocity ratio among bodies (1) & (2) is to remain constant the location of point P must remain fixed because O1 & O2 already have fixed positions. Hence, while the two bodies (1) & (2) transmit motion, the common normal at the point of contact must always intersect the line joining the centres of rotation at a fixed point to have constant velocity ratio.