Calculation of Support Reactions:

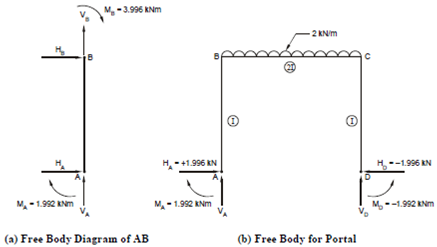
The support is fixed hence, it will be subjected to three reactions, sign conventions being horizontal reaction H_A (→ positive), V_A (↑ positive) and M_A (positive). From the above result M_A = + 1.992 kNm.

Considering the free body diagram of vertical member AB (Figure 20(a)), we find that it is acted upon by clockwise moments of M_A = + 1.992 and M_B = + 3.996 kNm at ends A and B respectively; in addition to the unknown reactions H_A, V_A at end A and H_B, V_B at end B. Taking moments about the point B, we have 1.992 + 3.996 - H_A × 3 = 0, giving H_A = 1.9968 kN and is acting toward right as shown.

By consideration of symmetry (or calculation if you so like), the horizontal reaction at D will be of same magnitudes, but opposite in direction. For finding VA, taking moments of all the forces acting on the frame as shown in Figure 20(b) about the point D, we have

+ 1.992 - 1.992 + V_A × 6 - (2 × 6) × 3 = 0

giving V_A = 6 kN.

The frame with the reactions and loading is shown in Figure 21(a). By vertical equilibrium of whole frame

V_A + V_D = 2 × 6

∴          V_D = 6 kN.

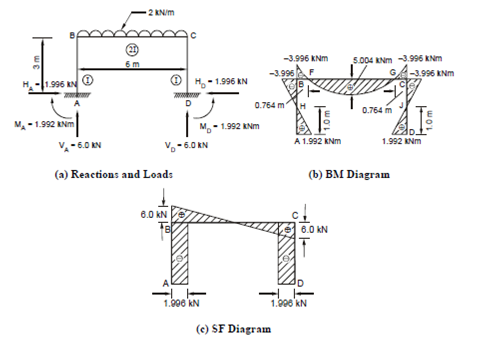
(a) While drawing the BM diagram, for the beam BC, the same convention is used for sagging and hogging bending moments; namely the positive sagging moment is drawn below (- ve) the reference line, i.e. on which side of the beam while fibres are in tension, and negative (hogging) moments are drawn above the line where fibres are in tension in this case.