Determination of 'n' and Reversibility:

It follows from the Eq. (8.13) while a plot of log (i/i_d - i) is plotted against the corresponding potential of the electrode on the increasing portion of the wave, a straight line will be acquired. A slope of this line will be equal to 0.05915/n from that 'n' could be determined. If 'n' is an integer value we could conclude in which the electrode reaction responsible for this wave is reversible. If a slope of log plot is bigger than the expected or 'n' is not integer value then the wave is irreversible or is a proof of the existence of a few slow steps in the over-all electrode reaction. In like these cases the waves are more drawn-out than reversible waves, or the equation is

Ox + ne^- → Re d

A half-wave potential, E_1/2 for reversible wave is simply found from a log plot through interpolation to search the value of the potential while the log term is zero.

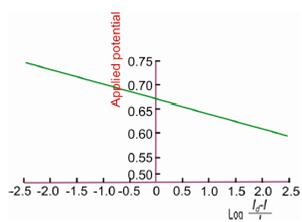
Figure: log plot of Cd(II) in 1M KCl

The other method to determine the reversibility of electrode reaction which is extremely simple and rapid is measuring the potential corresponding to ¼ and ¾ from the polarogram.

At E_1/4 for a reversible cathodic wave

 E _¼    = E _½ - (0.05915 /n) log (i_d / 4/i_d - i_d / 4)

= E _½ - 0.05915/n log 1/3

 and

E _¾      = E _½ - 0.05915/n log 3

so that

 E _¾   - E _¼    = - (0.05915/n) log 9 = - 0.0564/n

Therefore, the value of E_3/4 - E_1/4 is equal to - (56.4/n) mV and for reversible anodic wave it is equivalent to + (56.4/n) mV.