Isostress Condition
In previous section, the calculation presented is also applicable to the composite built of layers such as shown in Figure. Though, the same of composite is subjected to force normal to the layers in Figure. In this case each layer, having similar area of cross-section is subjected to similar stress, i.e.
σc = σ f = σm = σ ------------ (6)
In the composite, the total deformation shall be the sum of deformations in fibre and matrix
δc = δ f + δm ----------- (7)
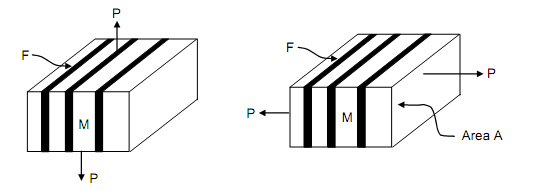
a) Isostrain (b) Isostress
Figure: Layered or Laminated Composite
If the total of the thicknesses of fibre layers is lf and that of matrix is lm, then thickness of the composite in the direction of force P is
lc = l f + lm ---------- (8)
From Eqs. (6), (7) and (8)
σ/ E(l f + lm ) = σ / E (l f ) + σ / E( l m )
Multiplying by A
A (l f + lm ) = l f A/ E f + lm A/ Em
1/E = l f A /Ef . 1 / Ef + lm A/(l f + lm ) A . 1/ Em
Identify that coefficients of 1 /E f and 1 /Em are respectively Vf and Vm volume ratios of fibre and matrix.
∴ 1 / E = V f / E f + Vm /Em -------------(9)
or, E = E f Em / (V f Em + Vm E f)
From above equation it is observed that if Vm = 0, E = Ef.
This may be regarded as extreme value. If we let matrix material for polyvinyl chloride and reinforcing material of glass fibre of which
Em = 350 MPa and Rf = 70,000 MPa, then
E = (70000 ×350) / (V f × 350 + Vm × 70000)
= 70000 / (V f + 200 Vm)
which means Vm is 200 times as effective as Vf in decreasing the fibre modulus of elasticity in a composite material. We may demonstrate the effect by giving many values of Vm as we did earlier in case of composite under isostrain loading. Following values of E are attained for different values of Vm.

For the sake of comparison verify the ratio of modulus of elasticity of a composite under isostrain condition (Estrain) to that under isostress condition (Estress). Given table shows the comparison and same has been plotted in Figure.
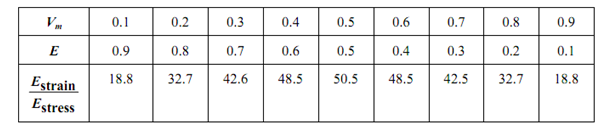
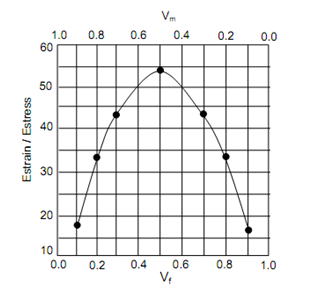
Figure: (a) Isostrain Condition – Modulus of Elasticity of Composite; (b) Isostress Condition – Modulus of Elasticity of Composite, and (c) Ratio of Modulus of Elasticity under Isostrain and Isostress Conditions
From above calculations it is clear that the highest value of modulus of elasticity under isostress condition is much small. It is because the fibres do not resist stress perpendicular to length. The situation is developed much if fibres are provided in two perpendicular directions. The nets of fibres are commonly utilized as reinforcing elements unless the design conditions need the part to carry only uniaxial load. It might also be noted that maximum stress that may be carried by a composite under isostress condition is find out by lowest of strength of fibre and matrix as the stress is to be similar in matrix and fibres. Even if modulus of elasticity of composite is higher than that of matrix in isostress condition, this is not of any use because matrix shall yield or begin to deform plastically at much lower stress value.