Broken Fibres

In isostrain analysis it was supposed that all fibres participated equally in carrying load. However, some fibres might be broken in which case these fibres might not carry any force. The area of matrix sustaining force remains similar but that of the fibres changes. Therefore the proportionate contribution of the matrix in load carrying ability of the composite increases. This is not difficult to conclude that the highest fraction of fibre that may be tolerated to have broken in composite shall bring matrix under its permissible stress. If the fraction of broken fibres exceeds then this value the matrix shall be subject to stress higher than its capacity and therefore composite shall fail.

                                                       Figure: Composite with Broken Fibre

We suppose that the composite in Figure was made with volume fractions V_f and V_m for fibre and matrix with V_f + V_m = 1. Let us say a fraction x of fibre is broken so that the volume fraction of fibre changes to V ′_f = V_f - x and that of matrix becomes V′_m = 1 - V_f + x. The breaking of fibres reduces the area of fibre but does not enhance the area of the matrix. Therefore the gross areas of cross-section of composite reduces and it shall now be (1 - x) of the original area. Therefore, the stress in the composite shall increase. If the stresses are σ′_c, σ′_m and σ′_f in composite, matrix and fibre respectively after the fibres have broken, then

                                     σ′_c (1 - x) = σ′_m (1 - V _f + x) + σ′_f (V _f - x)

or,

                                              σ′_c - σ′_m (1 - V _f ) - σ′_f  V _f

                                                     = (σ_c + σ′_m - σ′_f ) x

or,            σ′_c - σ′_m + V _f

                                                x = (σ′_m - σ′_f )                           ----------- (10)

                                                 σ′_c + σ′_m - σ′_f

Also note down that to satisfy the condition of isostrain the strains in matrix & fibre are similar, i.e.

                                             σ′_f / E _f  = σ′_m / E_m                  -------------- (11)

or                                            σ′ f     = σ′ m  E_f / E_m                 

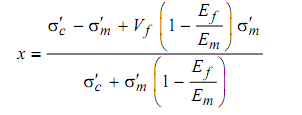
∴                           x    = (σ′c - σ′m + V f(1 - (Ef/Em) σ′m )/ (σ′c + σ′m (1- (Ef /Em)     ----------------(12) 

Eq. (12) may be directly used for discovering the maximum fraction of broken fibres. This information may be utilized in several ways, one of which is the quality control of the composite. It shall be known in advance as to what percentage of fibres in a composite might be tolerated so that a desired strength of a composite is attained. Solved problem in the following instance shall demonstrate the above fact.