Torque acting on the shaft:

The torque acting on the shaft

T = T₁  + T₂

where, T₁ = Torque for elastic deformation from r = 0 to r = r_γ, and

T₂ = Torque for plastic deformation from r = r_γ  to r = d/2 .

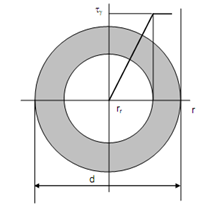
Figure

Both T₁ and T₂ may be calculated by considering stress on elementary ring of depth dr at radius r.

τ is the stress acting on the elementary ring in elastically deformed zone, i.e. 0 ≤ r ≤ r_γ and τ is the stress acting in plastically deformed zone, i.e. r _γ  ≤ r ≤ d/2 .

At         r = r_γ , τ= τ_γ

That means in elastic region.

τ= (τ_γ/ r_γ )r

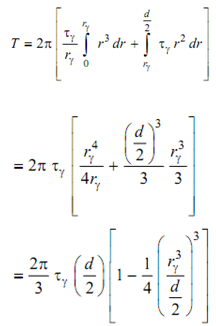
Utilizing Eq. (40), or

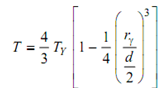
Here, T_γ is the highest elastic torque carried by the cylindrical shaft. When entire section is deformed plastically r_γ = 0, then plastic torque

T_p  =4/ 3 T_Y

In case of plastic deformation the straight radius of the section remains straight as in elastic deformation which means that shearing strain

           γ= r θ / l

or         r = l γ / θ

At the onset of yielding the angle of twist is θ_γ and shearing strain γ = γ_Y

 ∴         d/2 = l γ_Y / θ_Y

 If plastic deformation has developed to r_Y only

r _Y  = l γY/θ

 Taking ratio of Eqs. (3) and (4)

r_Y / (d/2)   = θ_Y    / θ

Substituting for r_Y /(d/2) in Eq.  we have

T =       (4/3) T_Y  [ 1- (1/4)( θ_Y /θ)³ ]