Simple pendulum:

A simple pendulum can be considered to be a point mass suspended from a string or rod of the negligible mass. A simple pendulum consists of a heavy mass suspended by an inextensible or non-elastic thread from the fixed point.

The length of pendulum is the distance from the point of the suspension to the center of gravity of bob. The resting position of a simple pendulum is called as the mean position. It is a resonant system with the single resonant frequency. For small amplitudes, the period of such type of pendulum can be approximated by:

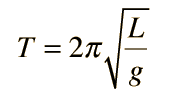
A simple pendulum comprises of a mass m hanging from the string of length L and fixed at the pivot point P. When displaced to an initial angle and released, the pendulum will swing back and forth with the periodic motion. By applying Newton's 2nd law for the rotational systems, the equation of motion for the pendulum can be obtained as,

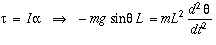
And rearranged as.

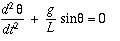
If the amplitude of angular displacement is small enough that the small angle approximation holds true, then the equation of motion reduces to the equation of the simple harmonic motion.

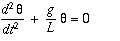
The simple harmonic solution we obtain is

θ(t) = θ₀ cos(ωt+φ)