Matrices and Determinants

These are the coefficients of the independent variables. aij might be constant or functions of some parameter. A more convenient form might be got for the above equations by evaluating them in matrix form

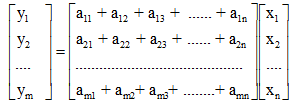
                        Or                  Y =     A X

            Matrix   A=[aij] is known the characteristic matrix of the system; its dimension or order is mentions like

                                                            d(A) =m x n

            Here m is the number of rows and n is the equal to number of columns.

            Attached to any matrix A=[aij] is a definite scalar function of the aij, known the    determinant of A. This number is mention like

                                                             det A or |A| or ?A or

                                                a11 +a12 +a13+ ... +a1n       

                                                a21 +a22 +a23 + ...+a2n                 

                                                ...........................        

                                                 am1 +am2+am3+...+amn           

By applying these concepts to our analysis, the clarification of simultaneous equations becomes very simple. Let's consider some examples of KVL & KCL and apply this particular technique and we will see that the simplification of our equations shall become tremendously easy.