Sine waves as circular motion:

A sine wave depicts the most efficient possible way which a quantity can alternate back and forth. The reasons for this are complex, and a thorough discussion of it would get into the fuzzy thought territory where science begins to overlap with esthetics, mathematics, and philosophy. You need not worry about it. You may recall, however, that a sine wave has just one frequency component, and represents the pure wave for this reason.

Suppose that you were to swing the glowing ball around at the end of a string, at the rate of 1 revolution per second. The ball would describe the circle in space.  Suppose that you swing the ball around such that it is always at same level; so that it takes a path which lies in the horizontal plane. Imagine that you perform this in the perfectly dark gymnasium. Now if a friend is standing some distance away, with his or her eyes right in plane of the path of ball, what will friend see? All that will be visible is glowing ball, oscillating.  The ball will appear to move toward the right, slow down, then stop and reverse the direction of it, going back towards the left. It will move faster, then slower again, reaching the left-most point, at which it will stop and turn again. This will go on, with the frequency of 1 Hz, or a complete cycle per second, as you are swinging the ball around at 1 revolution per second.

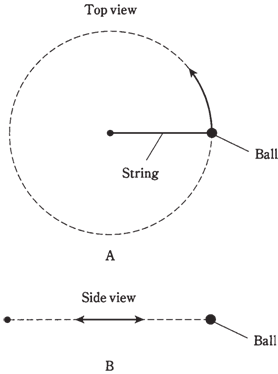
Figure--   Swinging ball and string. At point A, as seen from above; at point B, as seen from edge-on.

Graph the position of the ball, as seen by your friend, with respect to time, the result will be a sine wave shown in the figure given below. This wave has the same characteristic shape as all the other sine waves.

Some sine waves are taller than the others, and some are stretched out horizontally more than others. But the general wave form is same in each case. By multiplying or dividing the amplitude and the wavelength of any sine wave, it can be made to fit along the curve of any other sine wave. The standard sine wave is function y = sin x in (x,y) coordinate plane.

You might whirl the ball around faster or slower than one revolution per second. The string might be made longer or shorter. This would alter the height and or the frequency of sine wave graphed in the Figure. But fundamental rule would always apply which states that the sine wave can be reduced to the circular motion.