Degrees of phase:
If you wondered why phase is spoken of in the terms of angular measure, the reason should be clearer now. A circle has 360°

Figure--Position of ball as seen edge-on, as the function of time.
. A sine wave can also be represented as the circular motion. Exact moments along with the sine curve correspond to the specific angles, or positions, around the circle.
Figure given above shows the way a rotating vector is used to represent the sine wave. At point A, the vector points east, and this is assigned value of 0 degrees, where the wave amplitude is zero and is positively increasing. At point B, the vector points north; this is the 90° instant, where the wave has attained its maximum positive amplitude. At point C, the vector points west. This is 180 °, the instant where the wave has gone back to zero amplitude, and becomes more negative. At point D, the wave points south. This is 270°and represents the maximum negative amplitude. When the full circle has been completed or 360 °, the vector once again points east. Therefore, 360 degrees is same as 0 degrees. Actually, a value of x degrees represents the same condition as x plus or minus any multiple of 360 °.
The 4 points for the model of Figure given below are shown on the sine wave graph given below.
You can think of vector as going around, at a rate that corresponds to one revolution per cycle of wave. If the wave has the frequency of 1 Hz, the vector goes around at the rate of a revolution per second (1 rps). If the wave has the frequency of 100 Hz, the speed of vector is 100 rps, or the revolution every 0.01 second. If the wave is 1 MHz, then speed of the vector is around 1,000,000 or 106 rps, and it goes once around every 106, or 0.000001, second.

Figure-- Vector representation of sine wave at the start of a cycle (A), at 1⁄4 cycle (B), at 1⁄2 cycle (C), and at 3⁄4 cycle (D).
The peak amplitude of wave can be thought of in the terms of the length of the vector. In the Figure, time is represented by angle counterclockwise from due east, and amplitude is independent of the time. This differs from more common rendition of the sine wave, such as the one in the Figure given below.
In the sense, the force causes the wave is always there, whether there is any instantaneous voltage. The wave is created by the angular motion of this force. This is apparent in the rotating-vector model. The reasons for thinking of alternating current as a vector quantity.
If the wave has a frequency of f Hz, then vector makes a complete 360° revolution every 1/f seconds. The vector goes through 1°of phase every 1/(360f) seconds.
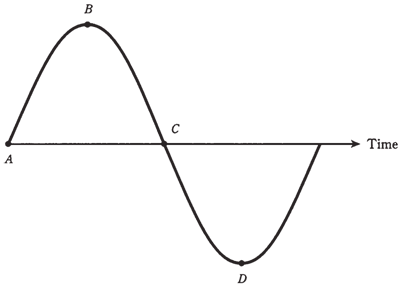
Figure-- The four points for the model of, shown on a standard amplitude-versus-time graph of a sine wave.