Short-run Equilibrium of Firm:

As the firms under perfect competition are all identical, we can consider any one firm to represent the rest.

Let q = quantity of output produced by the firm       

C (q) = cost function
        p = price per unit of the product
        Π = profit.
Given these variables, the profit function of the firm would be,
                Π  = TR - TC = pq - C (q) and
to maximise it we differentiate  ∏ with respect to q and set the derivative equal to zero,

       ∂Π/∂q = p - ∂C/∂q = 0

or, p = MC (the marginal cost)

Under perfect competition, a firm would produce up to that level of output where p equals MC.  As the marginal revenue (MR) is equal to p, we have P = MC = MR at the profit maximising level of output

Diagrammatically we can represent these conditions  as follows:

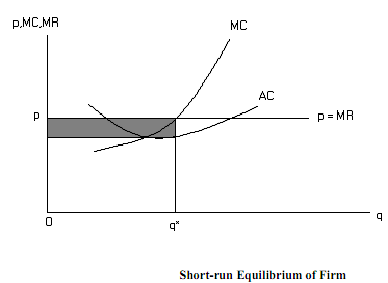
In the diagram, AC represents the short-run average cost curve of the firm and MC the marginal cost. MC intersects AC at the latter's minimum point. Given the price, p, MR and AR curves are given by the horizontal price line. The equilibrium point of the firm is the point where the MC curve cuts the price line. Dropping a perpendicular from the intersection point to the horizontal axis, we get the equilibrium output oq*. The shaded region represents the profit accruing to the firm with oq* level of output.

Short-run profit maximisation:

The point of intersection of MR and MC gives the stable equilibrium point. For any point other than q* the firm would go back to the equilibrium output level. For a q < q*, MC < MR, so that q would rise and for any q > q*, MC > MR, q would fall.
In the short-run, the firm would make a profit given by the shaded area. This will be true for all the firms, because the firms are all identical.