Pascal's Law For Incompressible Liquids:

Imagine a watertight, stiff container. Assume that there are two pipes of unequal diameters running upward out of this container. Visualize that you fill the container with an incompressible liquid like water so that the container is entirely full and the water rises partway up into the pipes. Assume that you put pistons in the pipes so that they make ideal water seals, and then you leave the pistons to rest on the water surface. The figure is as shown below.

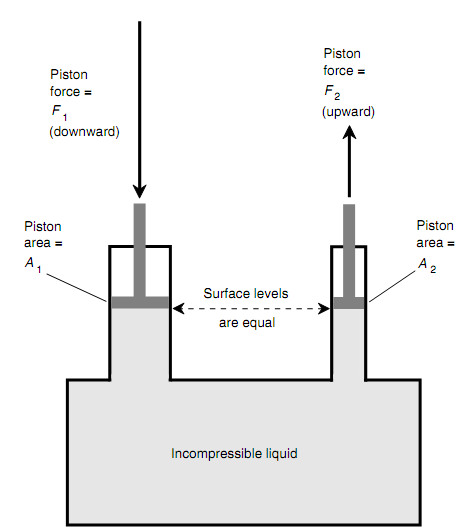
Figure: Pascal's law for confined, incompressible liquids. The forces are directly proportional to the regions of the pistons.

Since the pipes have unequal diameters, the surface regions of the pistons are dissimilar. One of the pistons has region A₁ (in meters squared), and the other has region A₂. Assume that you push downward on piston number 1 (i.e., the one whose region is A₁) with a force F₁ (in newtons). Determine the upward force F₂ is produced at piston number 2 (i.e., the one whose region is A₂)? Pascal's law gives the answer: The forces are directly proportional to the areas of the piston faces in terms of their contact with the liquid. In the illustration shown by the above figure, piston number 2 is smaller than piston number 1, therefore the force F₂ is proportionately less than the force F₁. Mathematically, the equations below can hold both as:

F₁/F₂ = A₁/A₂

A₁F₂ = A₂F₁

Whenever using either of these equations, we should be consistent with units throughout the computations. Additionally, the top equation is meaningful only as long as the force applied is nonzero.

PROBLEM:

Assume that the areas of the pistons shown in given figure are A₁ = 12.00 cm² and A₂ = 15.00 cm². If you press down on piston number 1 with a force of 10.00 N, determine how much upward force will outcome at piston number 2?

SOLUTION:

Firstly, you may think that we have to convert the areas of the pistons to meters squared in order to resolve this problem. In this situation, though, it is enough to find the ratio of the areas of the pistons as both areas are specified to us in the identical units:

A₁/A₂ = 12.00 cm²/15.00 cm²

           = 0.8000

Therefore we know that F₁/F₂ = 0.8000. We are given F₁ = 10.00 N, therefore it is easy to resolve for F₂:

10.00/F₂ = 0.8000

1/F₂ = 0.08000

F₂ = 1/0.08000 = 12.50 N

We are permitted to four significant figures throughout this computation as all the input data were given to this degree of accuracy.