Elasticity of Solids:

Some of the solids can be compressed or stretched more easily than others. A piece of copper wire, for illustration, can be stretched, though a similar length of rubber band can be stretched much more. Though, there is dissimilarity in the stretchiness of these two substances which goes beyond mere extent. When you let go of a rubber band after stretching it, it will spring back to its initial length, though if you let go of a copper wire, it will remain stretched.

The elasticity of a substance is the extent of its capability to return to its original dimensions after a sample of it has been compressed or stretched. According to this definition, rubber has high elasticity, and copper has low elasticity. Keep in mind that elasticity, defined in this manner, is qualitative (it says somewhat about how a substance acts) though is not truly quantitative (we are not assigning particular numbers to it). Scientists can and at times do define elasticity according to the numerical scheme, though we won't worry about that here. It is worth talking about that there is no such thing as a completely elastic or perfectly inelastic material in the real world. Both these extremes are hypothetical ideals.

This being said, assume that there does exist a perfectly elastic substance. Such a material will follow a law concerning the extent to which it can be compressed or stretched whenever an external force is applied. This is known as Hooke's law: The extent of stretching or compression of a sample of any substance is directly proportional to the applied force. Mathematically, when  F is the magnitude of the applied force in newtons and s is the amount of stretching or compression in meters, subsequently

s = kF

Here k is a constant which depends on the substance. This can be write in vector form as

s = kF

to point out that the stretching or compression occurs in the similar direction as the applied force.

Perfectly elastic stuff cannot be found in the real world, though there are abundance of materials which come close sufficient and hence Hooke's law can be considered valid in a practical logic, given that the applied force is not so great that a test sample of the material breaks or is crushed.

PROBLEM:

Assume that an elastic bungee cord has almost perfect elasticity as long as the applied stretching force does not surpass 5.00 N. Whenever no force is applied to the cord, it is 1.00 m long. Whenever the applied force is 5.00 N, the band stretch to a length of 2.00 m. Determine how long will the cord be when a stretching force of 2.00 N is apply?

SOLUTION:

By applying 5.00 N of force causes the cord to become 1.00 m longer than its length whenever there is no force. We are sure that the cord is "perfectly elastic" as long as the force does not surpass 5.00 N. And hence, we can compute the value of the constant k, known as the spring constant, in meters per newton (m/N) by rearranging the previous formula:

s = kF

k = s/F

k = (1.00 m)/(5.00 N) = 0.200 m/N

given that F <=5.00 N. And hence, the formula for displacement as a function of force becomes

s = 0.200F

When F = 2.00 N, then

s = 0.200 m/N x 2.00 N = 0.400 m

This is the additional length by which the cord will "grow" whenever the force of 2.00 N is applied. Since the original length, without applied force, is 1.00 m, the length with the force apply is 1.00 m + 0.400 m = 1.400 m. Hypothetically, we ought to round this off to 1.40 m.

The behavior of this bungee cord, for stretching forces among 0 and 5.00 N, can be demonstrated graphically as shown in figure below. This is a linear function; it emerges as a straight line whenever graphed in standard rectangular coordinates. When the force surpasses 5.00 N, according to the specifications for this specific bungee cord, we have no guarantee that the function of displacement versus force will stay linear. In the extreme, when the magnitude of the stretching force F is great adequate, the cord will snap, and the displacement s will skyrocket to undetermined values.

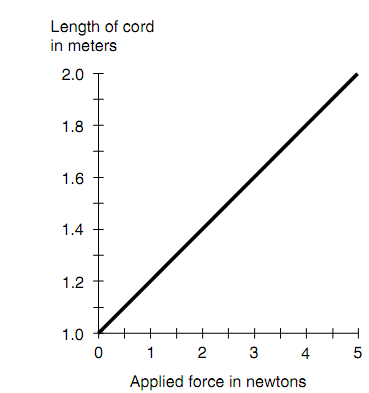
Figure: The function is linear within the range of forces shown here.

In liquid state or phase, a substance has two properties which differentiate it from the solid phase. At first, a liquid changes shape therefore it conforms to the inside boundaries of any container in which it is placed. Secondly, a liquid placed in an open container (like a jar or bucket) flows to the bottom of the container and build up a defined, flat surface. At least this is the manner a sample of liquid behaves in an atmosphere where there is gravity.