Influence of this choice of blending function:

Let us investigate the influence of this choice of blending function: set f₁ = g₁ =

and f₂ = g₂ = in (41). The cross boundary derivative along, say, u = 0, now becomes :

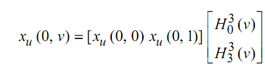
all other terms vanish since 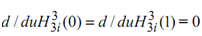for i = 0 and i = 1.

Therefore, the only data that influence p_u along with u = 0 are the two tangents p_u (0, 0) and p_u (0, 1) - we have attained our goal of making the cross boundary derivative along one boundary based only on information pertaining to that boundary. Along our new blending functions, the two patches from Figure would now be C¹.

Unluckily, the partially bicubically blended Coons patches, constructed as above, suffer from zero corner twists and therefore at the patch corners, these patches frequently seem to have "flat spots".

                  x_uv (i, j) = 0; i, j ∈ {0, 1}.

It is easily verified by simply taking the u, v-partial of Eq. (41) and evaluating at the patch corners. Now we shall modify the partially bicubically blended Coons patch to ignore the flat spots at the corners.