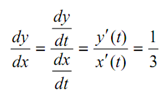Straight Line:

For the position vectors P₁ [1 2] and P₂ [4 3], measure the parametric representation of the line segment among them. Also calculate the tangent and slope vector of the line segment.

Solution

A parametric representation is following

P (t) = P₁ + (P₂ - P₁) t = [1 2] + ([4 3] - [1 2]) t          0 < t < 1

P (t) = [1 2] + [3 1] t   0 < t < 1

Parametric representations of the x and y components are following

x (t) = x₁ + (x₂ - x₁) t = 1 + 3t                      0 < t < 1

y (t) = y₁ + (y₂ - y₁) = 2 + t

The tangent vector is attained by differentiating P (t). Specifically,

      P' (t) = [x' (t)  y' (t)] = [3  1]

or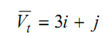     

Here,    is the tangent vector and i, j are unit vectors in the x, y directions, respectively.

The slope of the line segment is following