Parametric curve representation:

As a point on a parametric curve is described by a single value of the parameter, the parametric form is axis-independent. The curve end points & length are fixed by the parameter range. Frequently it is convenient to normalize the parameter range for the curve segment of interest to 0 ≤ t ≤ 1. Since a parametric curve is axis-independent, it is easily manipulated by utilizing the affine manipulation transformations.

The simplest parametric 'curve' representation is for a straight line. For two position vectors P₁ & P₂, a parametric representation of the straight line segment among them is

P (t) = P₁ + (P₂ - P₁) t   0 ≤ t ≤1

As P(t) is a position vector, each of the components of P(t) has a parametric representation x(t) and y(t) among P₁ and P₂, i.e.

x (t) = x₁ + (x₂ - x₁) t    0 < t < 1

y (t) = y₁ + (y₂ - y₁) t

Comparisons of nonparametric & parametric representation of a circle in the first quadrant are illustrated in Figure. The nonparametric representation of the unit circle in the first quadrant specified by

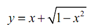                                                                   0 ≤ t ≤ 1

is illustrated in Figure (a). Equal incremental in x were utilized to get the points on the arc. Note down that the resulting arc lengths along the curve are unequal. A poor visual representation of circle result. Furthermore, calculation of the square root is computationally expensive.

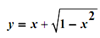            0  ≤  t  ≤  1           x = cos θ,  y = sin θ       0 ≤ θ ≤2π

 (a): Circle Representations for the First Quadrant