Circle Representations:

As a point on a parametric curve is indicated through a single value of the parameter, the parametric form is axis-independent. The curve ending length and points are fixed by the parameter range. Frequently it is convenient to normalize the parameter range for the curve segment of interest to 0 < t < 1. As a parametric curve is axis-independent, this is easily manipulated utilizing the affine manipulation transformations.

The easiest parametric 'curve' representation is for a straight line. For two location vectors P₁ and P₂, a parametric representation of the straight line segment among them is

P (t) = P₁ + (P₂ - P₁) t 0 < t < 1

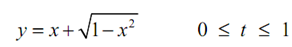
As P(t) is a position vector, each components of P(t) contain a parametric representation x(t) and y(t) among P₁ and P₂, that means

x (t) = x₁ + (x₂ - x₁) t  0 < t < 1

y (t) = y₁ + (y₂ - y₁) t

A comparison of parametric and nonparametric representation of a circle in the first quadrant are illustrated in Figure 4. The nonparametric representation of the unit circle in the first quadrant provided by

is illustrated in Figure 4(a). Equal incremental in x were utilized to get the points on the arc. Notice down that the resulting arc lengths along with the curve are unequal. A poor visual representation of circle results. Additionally, calculation of the square root is computationally costly.

 Figure : Circle Representations

The standard parametric form for a unit circle is following

x = cos θ          0 < θ < 2π

y = sin θ

or         P (θ) = [x y] = [cos θ sin θ]  0 < θ < 2π

here the parameter θ is linked with the geometric angle calculated counter clockwise from the +ve x-axis. Equal enhance in the parameter θ for the range 0 < θ < π/2 were utilized to get points on the arc illustrated in Figure 4(b). As for this parametric representation, equal parameter enhancement generate equal arc length along the circumference of the circle, the appearance is fairly good.