Osmotic equilibrium:

It is probable to derive, from purely thermodynamic considerations, an expression for osmotic pressure within terms of measurable solution parameters. At any constant temperature and pressure of one atmosphere, transfer of solvent within solution occurs since the molar free energy of the pure solvent, μ⁰, (standard chemical potential of the solvent) is greater than the partial molar free energy of the solvent in the solution μi. To bring equilibrium among the two and therefore, stop osmosis, it is essential to increase the value of μi   through applying higher external pressure on the solution. If this rise in free energy is Δμi, then the condition for osmotic equilibrium must be

µ_i⁰ =  μi     + Δ_μi

and hence

µ_i⁰ -  μi     = Δ_μi

The chemical potential (μi) of elements, i, in a solution is defined in terms of Gibbs free energy (G) through the relation

dG =  SdT  +  VdP  +∑_i μ_i dN_i

where, S is the entropy, T is the absolute temperature, V is the volume , P is the pressure and N_i  is the number of moles of component, i.

From Eq.,

μ_I   =   (∂G/ ∂N_i )_T,P,N

and

V   =  (∂G/ ∂P)_T,

where, N represents the entire set of N's and Nj represents all N's except N_i..

Differentiating Eq. with respect to N_i

(∂ 2G/∂ N_i ∂P)T, N   = (∂μi  /∂P)T,N   = (∂V/∂N_i )T,P,N     =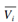

where, 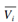 is the partial molar volume of component, i.

 The thermodynamic activity, ai of elements, i is associated to its chemical potential μ_i through the relation

μ_i⁰      =    μ_i *   + RT ln a_i

where, R is a gas constant.