Computing the activity of water:

For computing the activity of water within the solution, a_w, the vapour pressure data are needed. Often aw is calculated from the relation

a_w    = P_w / P^*_w

while, P_w  is the vapour pressure of water in equilibrium with the solution at a specified temperature, while Pw^* is that of pure water at the same temperature.

Here If the solute is volatile, the partial vapour pressure of water must be used for P_w.

Substituting Eq. 2 in Eq. 3, we get

Π V_w    = RT ln ( P_w  / P^*_w)

Eq. can be reduced to a simpler form from the special case of dilute solution of binary electrolyte obeying Raoult's law. For such solution

where, N₁  and N₂   denote the mole fraction of solvent and solute, respectively. Eq.  can be written in terms of solute, the mole fraction as follows:

If ln ( 1- N₂ ) be expanded in series, then for dilute solutions all terms beyond the first can be neglected, and ln (1-N₂) becomes - N₂  which is equal to n₂/n₁ where, n2 is the number of moles of solute in n₁  moles of solvent. Therefore,

Π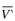_w  = RT n₂/n₁

and     Π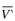_w  n1    = n2 RT

But  _w n₁ is the total volume of solvent containing n₂ moles of solute, which for dilute solutions is essentially the volume of the solution. as a result,

 ΠV = n₂  RT

or alternately

Π =     cRT

where, c is the molarity of the solution. Eq. is well known as van't Hoff's equation for ideal solutions. For electrolytes that ionise in solvent/ water, the observed osmotic pressure is more than what is predicted from molar concentrations data as the osmotic pressure is a colligative property of the solution which depends on the number of species within solution. Accordingly, a correction term called as van't Hoff factor is introduced in Eq. as follows.

Π = icRT

A van't Hoff factor is around equivalent to number of ions produced during ionization per molecule of the electrolyte.