Snell's Law:

If a ray of light meets a boundary among two substances containing various indices (or indexes) of refraction, the level to which the ray is bent can be established according to an equation termed as Snell's law.

Look at the figure shown below. Assume that B is a flat boundary among two media M_r and M_s, whose indices of refraction are r and s, correspondingly. Assume a ray of light crossing the boundary as shown below. The ray is bent at the boundary when the ray does not hit at a right angle, supposing that the indices of refraction r and s are dissimilar.

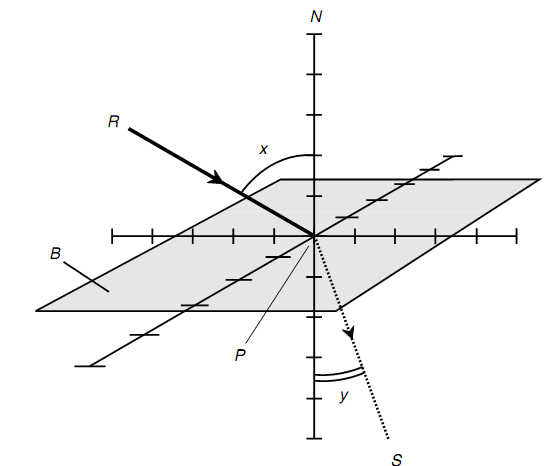
Figure: A ray passing from a medium with an associatively lower refractive index to a medium with an associatively higher refractive index.

Assume that r < s; that is, the light passes from a medium containing an associatively lower refractive index to a medium containing an associatively higher refractive index. Assume N be a line passing via some point P on B like N is common to B at P. Assume that R is a ray of light traveling via M_r which hits B at P. Let x be the angle that R subtends relative to N at P. Assume S be the ray of light that appears from P into M_s. Assume y be the angle which S subtends associative to N at P. Then line N, ray R, & ray S all lie in the similar plane, and y < x. The two angles x and y are equivalent if, though only if, ray R hits the boundary at an angle of incidence of 0°. The equation below holds for angles x and y in this condition:

sin y/sin x = r/s

This equation also can be stated like this:

s sin y = r sin x

Now look at the figure shown below. Again, assume B be a flat boundary among two media M_r and M_s whose fixed indices of refraction are r and s, correspondingly. In this situation, assume that r > s; that is, the ray passes from a medium containing an associatively higher refractive index to a medium containing a relatively lower refractive index. Assume N, B, P, R, S, x, and y be defined as in the previous illustration. As before, x = y if, though only if, ray R hits B at an angle of incidence of 0°. Then line N, ray R, and ray S all lay in the similar plane and x < y. Snell's law holds in this situation, just as in the location explained formerly:

sin y/sin x = r/s and s sin y = r sin x

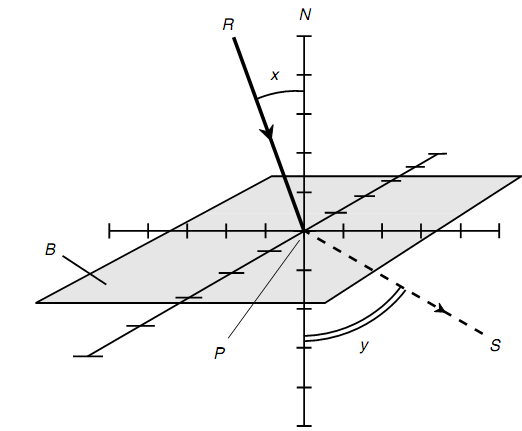
Figure: A ray passing from a medium with a relatively higher refractive index to a medium with a relatively lower refractive index.