Microscope Magnification:

Refer to the figure as shown below. Assume that f_o is the focal length (that is, in meters) of the objective lens and f_e is the focal length (that is, in meters) of the eyepiece. Suppose that the objective and the eyepiece are located all along a general axis and that the distance among their centers is accustomed for correct focus. Let us symbolized the distance (that is, in meters) from the objective to the real image it makes of the object under inspection. The microscopic magnification (i.e., a dimensionless quantity represented by m in this situation) is given by

m = [(s - f_o)/f_o)] [(f_e +  0.25)/f_e]

The amount 0.25 symbolizes the average close to point of the human eye that is the closest distance over which the eye can focus on an object: around 0.25 m.

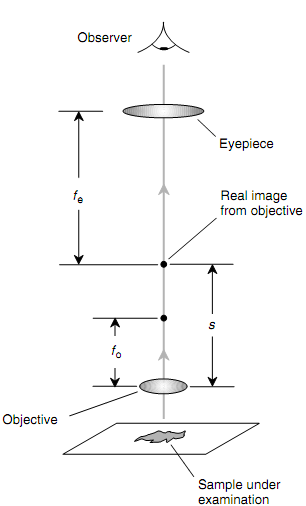
Figure: Computation of the magnification factor in a com- pound microscope.

The less formal technique of computing the magnification of a microscope is to multiply the magnification of the objective by the magnification of the eyepiece. Such numbers are given with objectives and eyepieces and are depend on the use of an air medium among the objective and the specimen, and also on the standard distance among the objective and the eye-piece. When m_e is the power of the eyepiece and m_o is the power of the objective, then the power m of the microscope as an entire is

m = m_em_o