Determining The Critical Angle:
Look at the figure shown below. The light passes from a medium containing an associatively higher index of refraction r into a medium containing a relatively lower index s. Hence, r > s. Since angle x rises, angle y approaches to 90°, and ray S get closer to the boundary plane B. If x, the angle of incidence, gets large sufficient (somewhere among 0° and 90°), angle y reaches to 90°, and ray S lies accurately in plane B. When angle x rises even more, ray R undergoes whole internal reflection at the boundary plane B. Then the boundary operates like a mirror.
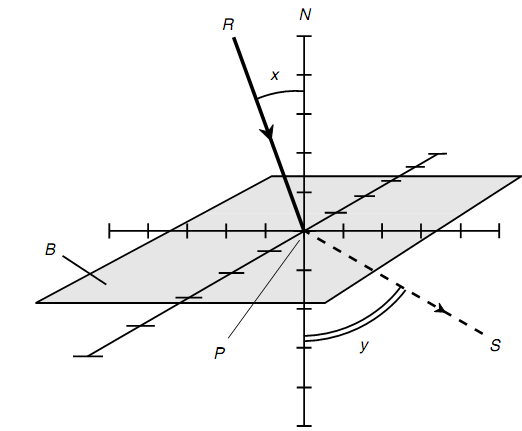
The critical angle is the largest angle of incidence which ray R can subtend associative to the common N without being reflected internally. Let us call this angle xc. The measure of the critical angle is the arcsine of the ratio of the indices of the refraction:
xc = sin-1 (s/r)