Bradley Aberration Method:
This method is based on the principle of relative velocity. When rain is falling vertically downward, a person standing on the road holds his umbrella vertically, but when he moves on the road, he holds his umbrella in a direction making some angle with the vertical.
This fact has been used in the measurement of the velocity of light by Bradley.
In 1729, Bradley observed that the angular elevation of a 'fixed' star varied slightly according to the position of the earth in its orbit around the sun. One day he was being rowed across a stream in a boat and he noticed that the boat drifted slightly downward. He at once thought that the difference between the actual and the observed angular elevation of the star was due to a combination of the velocity of the earth in its orbit and that of the velocity of light.
(i) When the earth is stationary.
(ii) When the earth is moving in its orbit.
(iii) Relative velocity of light with respect to the velocity of the earth.
If the earth were stationary, the telescope would have to point in the direction AS (analogous to umbrella when the men is stationary) to observe the star. But since the earth is moving with a velocity of 18.5 miles/second around the sun, the telescope would have to be directed along AS' to observe the star (analogous to umbrella when the man is moving in rain).
The direction of AS' is that of the relative velocity of light with respect to the earth. The angle between the true and the apparent direction of the star is 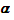 .
.
Here tan 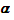 = v/c
= v/c
Since the angle is small, 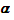 = v/c
= v/c
It will be clear from fig. that when the earth is at E1 it is moving towards the star, and at E2 it is moving away from the star. In these cases for the purpose of receiving light from the star it is stationary and there is no aberration. The aberration is maximum at E2 or E4 because the earth will be moving normal to the true direction of the star (analogous to the man moving normal to the direction of the rain).
The direction of motion of the earth is continually changing and the earth is moving in diametrically opposite directions at the spring and the autumn equinoxes. Therefore, on observing the position of the star near the zenith at these times, through a telescope it will occupy different positions with respect to the horizon. At the spring equinox, 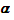 = v/c and at the autumn equinox,
= v/c and at the autumn equinox, 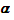 = v/c.
= v/c.
From the two positions of the telescope, the aberration can be calculated and it is equal to half the angle between the two positions of the telescope.
The angle 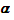 was found to be 20.24° of an arc and since v = 28.5 miles/second. However, aberration is independent of the distance of the star from the earth and should not be confused with parallax.
was found to be 20.24° of an arc and since v = 28.5 miles/second. However, aberration is independent of the distance of the star from the earth and should not be confused with parallax.