Aplanatic Points Surface:
A spherical refracting surface forms a point image of an axial point object only in the case of paraxial rays. When this condition is not satisfied, the refracted rays will not have a common point of intersection. The image of the axial point object will not be a point image. This departure from the ideal point image is termed as spherical aberration. However, this defect may be overcome by the use of an aplanatic surface. An aplanatic surface, with respect to two conjugate points is such that all the rays originating from one of the two points are reflected or refracted by the surface through the other point. Such a pair of points are termed as aplanatic foci or aplanatic points.
Let AP be the section of a refracting sphere with its centre at C. Consider the refractive index of the medium of the sphere asu2 and that of the medium outside the sphere as u2 where u1 > u2.
R is the radius of curvature of the sphere and O is the point object inside the sphere such that
![2065_aplanatic point surface].png](https://www.expertsmind.com/../CMSImages/2065_aplanatic point surface].png)
Let a ray OA be incident on the sphere at the point A and let AC be the normal at A.
Since u1 > u2, the ray is bent away from the normal and is refracted along AQ. Another ray OC incident normally at Pundergoes no deviation and passes straight. The two rays AQ and OP appear to diverge from I, which is the virtual image ofO. It can be easily proved that CI = u1R/u2 and all the rays starting from O, however oblique they may be, after refraction at the surface of the sphere will appear to diverge from I, i.e. I is a perfect image of a point object O free from spherical aberration.
Now, ∠ OAC = i ∠ NAQ = ∠ IAC = r,
∠ AOC = 
and, ∠ AIC = 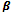
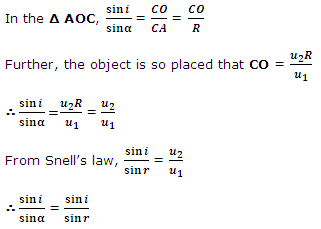
or,  = r
= r
Also in the Δ IAO, exterior ∠ AOC = 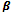 + ∠ AIO
+ ∠ AIO
∴  =
= 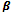 + r - i, But
+ r - i, But  = r
= r
∴ r = 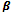 + r - i
+ r - i
or, 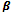 = i
= i
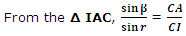
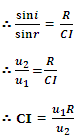
Thus, if CO = u2R/u1 = 1u2R, then the corresponding image lies at a distance Ci such that Ci such that CI = u1R/u2 = R/1u2and vice versa. This result is independent of the position of A. Hence all the rays, whether paraxial or peripheral, starting from O are refracted such that they appear to diverge from the point I. Therefore, I is the perfect point image of the point object O. As O and I are tow conjugate points free from spherical aberration, these are known as the aplanatic points of the spherical surface APB.
The property of aplanatic points has been utilized in the construction of high power microscope objectives.