Absolute Field Of View:

Whenever you look via the eyepiece of a telescope, you observe a circular patch of sky. Really, you can see everything in a cone-shaped area whose apex is at the telescope (as shown in figure below). The fixed field of view is the angular diameter q of this cone; q can be identified in degrees, minutes, and/or seconds of arc. At times the angular radius is identified rather than the angular diameter.

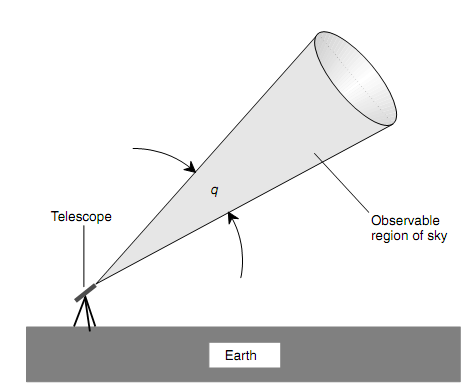
Figure: A telescope's fixed field of view q is measured in angular degrees, minutes, and/or seconds of arc.

The absolute field of view based on numerous factors. The magnification of the telescope is significant. When all other factors are held steady, the absolute field of view is inversely proportional to the magnification. When you double the magnification, you cut the field in half; when you decrease the magnification to one-quarter of its preceding value, you raise the field by a factor of 4.

The viewing angle-which is the apparent field of view-offered by the eyepiece is significant. Some kinds of eyepieces contain a wide field, like 60° or even 90°. The others have narrower evident fields, in some situations less than 30°.

The other factor which affects the absolute field of view is the ratio of the objective diameter to its focal length. In common, the larger this ratio, the wider is the greatest absolute field of view which can be acquired with the telescope. Long, narrow telescopes contain the smallest maximum absolute fields of view; small, fat ones have the widest highest fields.

PROBLEM:

Determine how much more light can a refracting telescope with a 15.0-cm-diameter objective gather as compared with a refracting telescope containing an objective whose diameter is 6.00 cm? State the answer in percentage.

SOLUTION:

The light-gathering region is proportional to the square of the objective's radius. Hence, the ratio of the larger telescope's light-gathering region to the smaller telescope's light-gathering region is proportional to the square of the ratio of their objectives' diameters. Let us call the ratio k. Then in this situation,

k = 15.0/6.00 = 2.50

k² = 2.50²

   = 6.25

The bigger telescope gathers 6.25 times, or 625 percent, as much light as the minor one.