Sinusoidal Oscillator Using Op-amps:

Figure illustrates the popular Wien bridge sinusoidal oscillator circuit by using op-amps. As per the conventional analysis, we break the feedback loop at node x, and find out the open loop transfer function (OLTF) T(S) from which the condition of oscillation and frequency of oscillation are determined by applying Barkhausen's criterion, i.e.

                      ∠ T ( j ω) = 0 and | T ( j ω) | = 1

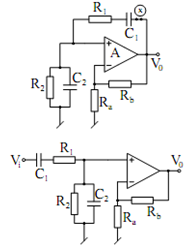
Figure: Wien Bridge Oscillator

By analysis, it is found that

T (s) =  (1+ R_b/ R_a )/ s² c² R²  + 3sc R + 1

 (for R₁ = R₂ = R and C₁ = C₂ = C)

By putting s = jw in Eq. (87) and using Eq. (86), you are advised to analyze the circuit given in Figure and check up that condition of oscillation is found to be (1 + (R_b / R_a ) = 3 , and that the oscillation frequency is found to be  f₀   = 1/2π RC.