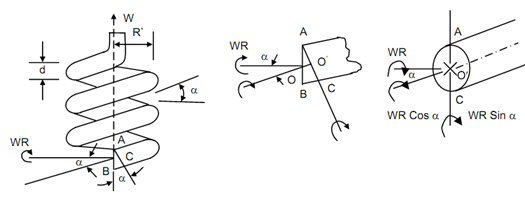
Spring Subjected to Axial Load:

The effect of axial W is to cause a moment T = W R around normal to AC. This moment is broken into two components, illustrated in Figure (c), viz. :

(a) W R cos α around axis which is perpendicular to the cross-section of the wire, and

(b) moment W R sin α around AO′C, a vertical axis of the cross-section and parallel to spring axis.

Therefore, apparently, an axial load W, on an open coil helical spring contains dual effect of

1. twisting the spring wire and inducing torsional shearing stress due to torque W R cos α, and

2. bending the spring wire and inducing bending stress because of BM W R sin α. Both torque and BM shall cause axial deflection.

(a)                                                       (b)                                     (c)

Figure: Open Coiled Helical Spring Subjected to Axial Load

Moment, M = W . R

Moment around the axis of the spring, (bending moment)

Mb = WR sin α

Moment around normal to the wire cross-section, (Torque)

T = WR cos α

Total length of the spring,

l = 2 π R n / cos α

Work done by axial load,

(1 /2 )W Δ

Strain energy due to bending,

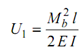
Strain energy because of torque,

U ₂  = T ² l / 2 GJ

Total strain energy,

U = U₁  + U ₂

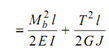
= (W ² R ² sin ² α) l/2 EI  + ((W 2 R ² cos² α) l )/2 GJ

U =         W²R²l [(sin²α)l/El+(cos²α)l/GJ]

This strain energy must be equal to the external work done.

∴(1/2) W Δ= (W ² R² l/2)[ sin ² α/EI + cos² α/GJ]

⇒         Δ= (W ² R² l)[ sin ² α/EI + cos² α/GJ]

= W R2 ( 2 π Rn / cos α) [ sin ² α/EI + cos² α/GJ]

I =  π/64 d⁴  ;  J =  (π/32) d ⁴

Substituting the values of I and J into the Eq. (26), we may get

Δ= 64 W R³ n sec α /d⁴  [2 sin 2 α/E + cos² α/G]

Both W R cos α (T) and W R sin α (Mb) shall cause rotation of the coil also.