Spring Subjected to Axial Couple:

Let an open coiled helical spring subjected to an axial couple 'T' as illustrated in Figure.

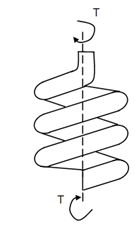
Figure

Consideration similar to these in Section shall show that an axial torque shall have two components T sin α and T cos α. Out of these the former refer  the torque which twists the spring wire, when the latter is the BM which bends the spring wire.

Bending moment component,

M _b  = T cos α .

This changes the curvature of coils.

Torque component,

T₁  = T sin α

It causes the twist in the wire.

Let φ = angle of twist at the free end of the spring, caused through axial torque, T

∴          Work done = (1 /2 )T φ

Strain energy due to BM , U₁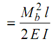 

or         U₁ = (T ² cos² α)/ 2 EI

Strain energy due to torque  

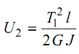
or         U ²  =(T ² sin ² α) / 2 GJ

Total strain energy,

U = U₁ + U₂

            =(T ² cos² α)/ 2 E I        +(T ² sin ² α)/2GJ

= (T ² l /2)[ cos² α  /EI + sin ² α/ G J]

Equating the total strain energy to work done, we may get

∴          φ= Tl   [ cos² α/EI + sin ² α/ GJ]

Where  l = 2 π R n cos α

I = π d ⁴/64          and  J = π d ⁴/32

φ= 64 T R n sec α/d⁴   [2 cos² α/E + sin ² α /G]

 Bending stress,

σ_b  =     M_b / z = 32 M b / π d ³

        = 32 T cos α / π d ³  

Shear stress,

τ= 16T₁ / π d ³

= 16 T sin α/  π d ³

Principal stress,

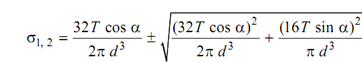
= (16T / π d ³) (cos α ± 1)

Maximum shear stress = ( σ₁ - σ₂ )/2

                                  = 16T / π d ³