Find out current:

An ohm meter with R_o = 30?, and full scale current I_m = 300 µA.  Find out I along with: 1) 0?, 2) 5?, 3) 10?, 4) 15?, and 5) 1 M? resistors across the meter terminal.

Solution:

First, deflection factor for every resistor must be found.

D = R_o/R_o +   R_x

1.         R_x   = 0?

D =   30 /30 =     1

2.         R_x   = 5?

D =      30/30 + 5 =0.86

3.         R_x   = 10?

D =      30/30 + 10 =0.75

4.         R_x   = 15?

D= 30/30+15 =0.67

5.         R_x   = 1 M?

D= 30/1 x 10⁶ =1 x 10^-6 = 0.000001 approximately 0

Then find out I through using:

I = D I_m

1.         R_x = 0?

I = (1) (300 x 10^-6) = 300 µA full scale deflection

2.         R_x = 5?

I= (0.86) (300 x 10^-6) = 258 µA

3.         R_x = 10?

I = (0.75) (300 x 10^-6) = 225 µA

4.         R_x = 15?

I = ( 0.67 ) ( 300 x 10^-6) = 201 µA

5.         R_x   = 1 M?

I = (0) (300 x 10^-6)      0 µA zero deflection

NOTE: As the resistance was increased from 0 to 5?   , meter current decreased through 42 µA. As same, while resistance was increased from 5 to 10?   , the current decreased by 33 µA.  Therefore, an ammeter scale used to measure resistance is nonlinear that was show in the figure.  The ohm meter scale is a reversal of the ammeter and voltmeter scales.  Alternatively, the zero resistance (R_x = 0) is at the right end of the scale and infinite resistance (R_x = 1 M   ) is at the left end of the scale.

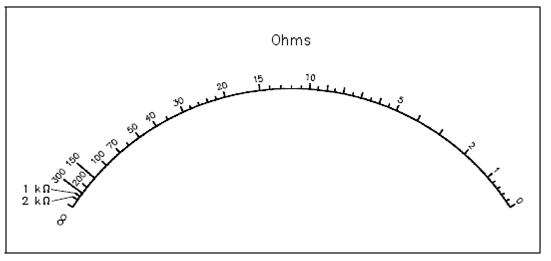
Figure: Ohm Meter Scale