Obstacles to Both Chaining and Ranging

Building is a typical instance of this obstacle. Referring to given figure, line AB is to be continued beyond the obstacle, say as GH. 4 possible methods are presented below:

(a) Set perpendiculars AC, BD such that AC = BD [Fig. (a)]. Extend the  line CD to F. Drop perpendiculars EG and FH to line CF such that EG = FH = AC. GH is the continuation of line AB and DE = BG.

(b) Referring from Fig. (b), set BC ⊥ to AB. choose D on extended line of AC. Set perpendicular DH such that AD = DH. Choose point E on DH such that DE = DC. Then arcs of length EG = BC and arc of length HG = AB are drawn from E and H respectively and G is located. GH is continuation of AB and

                                                               BG = CE.

(c) Referring to Fig. (c), C is located such that AC = BC = AB. Extend AC to D and construct equilateral triangle DEF. Extend DF to H such that DH = DA. Locate convenient point I on HD and construct equilateral triangle to locate G. Then GH is the continuation of line AB and length BG is given by

BG = AH - AB - GH = AD - AB - GH

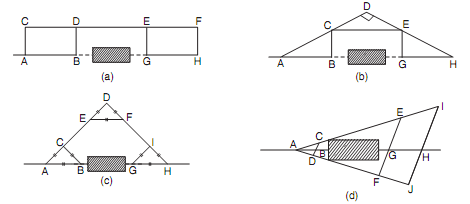
                                   Obstacles to both  ranging and chaining

(d) In the method shown in Fig. (d), points C and D are selected such that CBD is in a line. Extend AC to E and I such that AE = n × AC and AI = m × AC. Similarly Extend AD to F and J such that, AF = n × AD and AJ = m × AD. Locate G and H on lines EF and IJ such that, EG = n × BC and

IH = m × BC. Then GH is the continuation of line AB. Now, AG = n × AB

∴          BG = n × AB - AB = (n - 1) AB