Obstacles to Chaining

In this type the ends of lines are visible but chaining is blocked. Instance of such obstructions are lakes, ponds marshy land etc. Different geometric properties can be used to find obstructed length CB as shown in given figure.

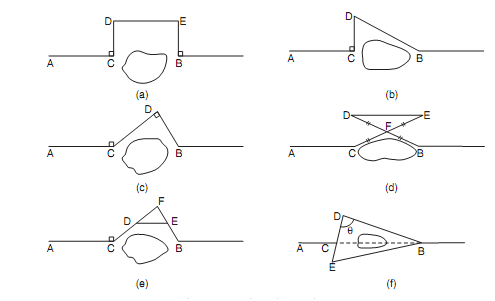
                                                           Obstacles to chaining

(a) Set CD and BE perpendiculars to AB, such that CD = BE. Then

             CB = DE                                                                                                                   [Fig. (a)]

(b) Set perpendicular CD to AB. Measure CD and DB. Then

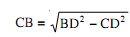                                                                                                  [Fig. (b)]

 (c) Set CD and DB such that DB ⊥ CD. Measure them. Then

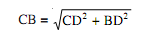                                                                                                         [Fig. (c)]

(d) Select a convenient point F. Set FE = CF and FD = BF. Then

                          CB = DE                                                                                          [Fig. (d)]   

 (e) Select a convenient point F. Locate D and E such that CF = n DF and BF = n EF. Measure

DE. Then,

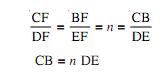                                      [Fig. (e)]

(f) Select points D and E on line passing through C [Fig. (b)]. Measure CD, CE, DB

and EB.

Then, from ?BDE,

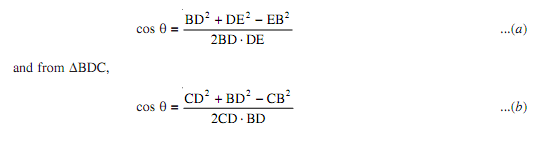
From eqn. (a), cos θ can be found and substituting it in eqn. (b), the obstructed length CB can be found