Find the support reactions:

A propped cantilever shown in Figure 6 carries the loads as shown. Find the support reactions and draw the BM and SF diagrams.

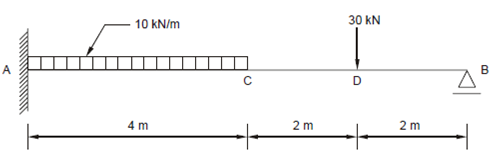
Solution

The reaction V_B at B due to the concentrated load of 300 kN is (using Eq. (2.14))

 V_B   = 30 × 6²/2 × 8³ (3 × 8 - 6) = 18.984 kN .

To search the reaction VB because of the uniformly distributed load we employ the following strategy :

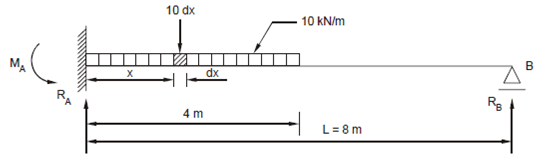
Consider a small strip dx at a distance x from fixed end A (Figure 7), as the load intensity is 10 kN/m the small load on this strip is 10 dx. We assume it to be a small concentrated load and the reaction Δ V_B due to this small load is (10 dx) x²/2 × 8³ [3 × 8 - x] , hence, the V_B due to the entire u d l will be obtained by integrating this expression over the range x = 0 to x = 4 m.

In other words

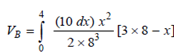
On rearrangement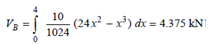

Thus the total reaction at B is given via

V_B = 18.984 + 4.375 = 23.359 kN.

The reaction at A is determined by ∑V ≡ 0 and is equal to

V_A  = (10 × 4 + 30) - 23.359 = 46.641 kN.

The fixing moment at A is

M_A  = 23.359 × 8 - 30 × 6 - 10 × 4 × 2 = - 73.128 kN m .

Here now the BM and SF diagrams could be easily drawn as shown in Figure 8.

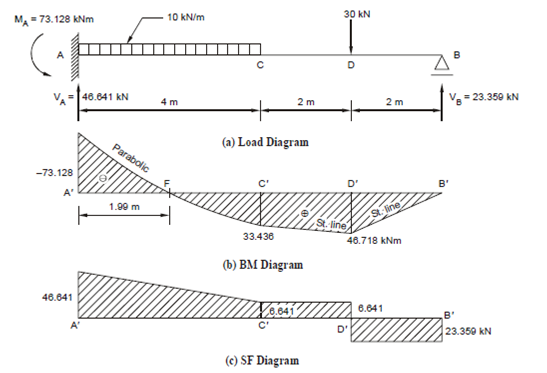
[Note : From A to C, the BM at any distance x is given by

Mx  = - 73.128 + 46.641 x - 10 x²/2. This is a parabola; which becomes 0 When x=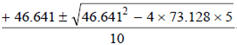

= 1.99 m. Hence, from A to F the bending moment is negative and for the rest of the beam it is positive.]