Charpy Impact Test

The Charpy impact test is represents on a square cross-section test piece, having a notch on one side in the central cross-section. The test piece is placed in charpy impact testing machine represented in following figure of The Specimen and Ball Indenter for Brinell hardness, such that swinging pendulum strikes the test piece at the central cross-section except on the opposite side of the notch. The test piece is simply holed on the platform of the machine as demonstrated in following figure (a). The commonly employed impact specimen is 10 millimeter square cross-section beam of 55 millimeter length, supported over 40 millimeter span and having a V-notch in the central plane that included angle is 45o, depth is 2 millimeter and root radius is 0.25 millimeter.

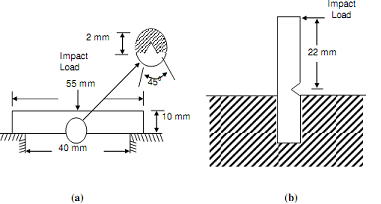
                                                               Figure: Impact Test Specimens

The charpy test machine shown in following figure is strong and rigid structure of two columns on a heavy base. A heavy swinging pendulum carries by columns at their top that swings on a frictionless pin, and hold platform at the bottom for the test piece. Even as the pendulum is in its vertical location its striking edge is level via the central cross-section of the test piece. The hammer or striker's mass is concentrated in vertical plane. A circular disc scale mounted centric along with the pin of the pendulum reads its position except is often calibrated in conditions of the potential energy of the pendulum.

To present the experiment the specimen is first placed into position via the assist of a centering device, the pendulum is held to and raised at its extreme position and after that allowed to fall. At its great position, h1 from the specimen, the pendulum has potential energy Wh1, here W is the weight of the pendulum. In this position the arm of the disc scale is in its great position, reading total amount of energy stored in the hammer. The speed of approximately released from its raised position and strikes the test piece at a speed of approximately 4.8 m/sec. Beneath this circumstance the test piece is forced to bend along with a rate of 103 mm/mm (sec) resulting into plastic deformation or instant fracture. The pendulum carries on its swing after fracturing or deforming the test piece and rises to height of h2. Subsequently, the pendulum swings back to oscillate pointer that does not swing back along with the pendulum. As before pointed out the disc scale is calibrated to read energy and the position of the dead pointer reads the difference of potential energies of the pendulum into two extreme positions consequent to h1 and h2. Naturally such difference of the energy is that that was absorbed in fracturing the test piece. Hence Uf denotes the impact roughness:

                                                          Uf = W (h1 - h2)....................Eq(1)

However, it may, be recognized that several energy loss may arise in the bearing of the pendulum and because of resistance also of air proposed to swinging pendulum. Such two losses may be found by simple experiment whether the pendulum is permitted to fall from is grater position with no placing the test piece in its path. The other great position to that pendulum rises will be slightly lowers than its initial position. The differentiation of the potential energies in two positions, denoted via the position of the dead pointer, is the loss of energy to air resistance and bearing friction. Such energy loss (UL) has to be subtracted from Uf to acquire corrected value of impact toughness as:

                                                          Uf = Wh1 - Wh2 - UL    . . . Eq(2)