Q:  Determine the voltage V_o by Norton's theorem .

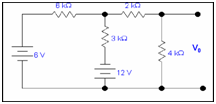
Sol:

            We have to estimate V₀ by Norton's theorem.

Step 1:  Replacing R_L with a short circuit to search I_N.

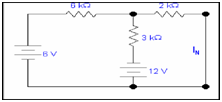
                        Here R_L is equal to 4k resistor.

Step 2:

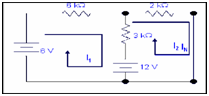
                        We have to calculate I_N.

                                    By applying KVL for loop1

                                                            6kI₁ +3k (I₁ -I₂) -12 -6 =0

                                                                            9kI₁ -3kI₂ = 18

                                    By applying KVL for loop 2

                                                             2kI₂ + 12 + 3k(I₂ - I₁ ) = 0

                                                                  -3kI₁ +5kI₂ = -12

                        Solving out equations for loop1 & loop2

                                                                         I₂ = -1.5mA

                                    Therefore,

                                                                        I_N = -1.5mA

Step 3: Determining R_N

To estimate R_N we short circuit all of voltage sources. 3k is in parallel to 6k & 2k is in series with them.

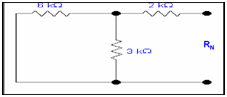
                                                6k||3k + 2k = (6k x 3k)/(6k+ 3k)  +2k

                                                                = 2k +2k = 4k = R_N

Step 4:

After estimating I_N & R_N, re-inserting the load resistance R_L in the circuit in parallel R_N and letting the I_N current source parallel along these two resistances.

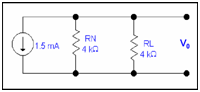
Current flow through R_L= (-1.5m x4k)/8k   (current division rule)

                                                             I₀=- 0.75mA

                                    Therefore

                                                           V₀  =  (-0.75m)(4k)= - 3volts