Q:  Determine the current I_o by using Norton's theorem.

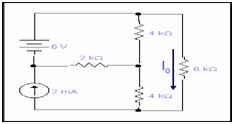
Solution:

We have to calculate I₀  using Norton's theorem.

Step 1:  Replacing R_L along with a short circuit to discover I_N. Here R_L is equal to 6k resistor.

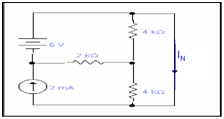
Step 2: Determine current I_N

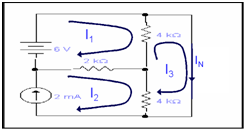
                        Through loop 2, we may write

                                                            I₂=2mA

            For path 1

                                    4k(I₁-I_N)+2k(I₁-I₂)-6=0

                                    4kI₁-4kI_N+2kI₁-2kI₂-6=0

                                                6kI₁-4kI_N-2kI₂=6

                        Putting the value of I₂ from above eq.

                                                    6kI₁-4kI_N-2k(2m) = 6

                                                            6kI₁-4kI_N = 10

            At Loop 3

                                                4k (I_N-I₂) +4k (I_N-I₁) =0

                                                4kI_N-4kI₂+4kI_N-4kI₁=0

                                                             -4kI₁+8kI_N=8

                        Solving out equations for loops 1 & 3

                                                12kI₁-8kI_N=20

                                               -12kI₁+24kI_N=24

                                                                16kI_N=44

                                                            I_N = 444/16 =2.75 mA

Step 3: Determining R_N

To determine R_N we have to short circuit all voltage sources & open the current sources.

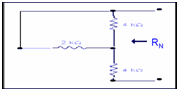
            For R_N

                                    2kII4k+4k =((2kx4k)/(2k+4k))+4k

                                            R_N = 5.33kΩ

Step 4:

After determining I_N & R_N, re-inserting the load resistance R_L in the circuit in parallel R_N and letting the I_N  current source parallel along these two resistances.

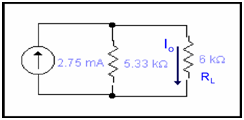
                                                I_o= (2.75m) (5.33k)x1/(6+5.33)k)

                                                 I_o =1.29mA