Normal Approximation to the Binomial Distribution:

The Binomial Probability

P(x₁ ≤ X ≤ x₂ ) = 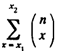 p^x q ^n-x

where x_l, x₂ are any two non-negative integers, represents the probability in that the binomial variable X suppose an integral value inside the interval [ x₁, x₂ ], where X is based on n Bernoulli's trials along with probability of success p. For given n and p, the probability could, no doubt, be computed using the summation in Equation. Therefore, this computation becomes numerically too complicated if n is large. The random variable X could be written as'

X=X₁+X₂...+X_n

where X_I, X₂, ..., X_n, are iid Bernoulli's variables every supposing the value 1 along with probability p or the value 0 with probability q ( - 1 -p ).

Additionally, E(X) = np and V(X) = npq and so

E(x¯) - p and v(x¯) = pq/n where x¯  = X/n

Thus, the central limit theorem gives for large n,

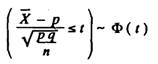
In other words, X/n approximately follows N (p, pq/n) since the inequality X ≤ x is equivalent to

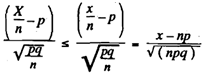
we have the cdf of X

F(x) = P(X ≤ x) ∼Φ (x-pq/√(npq))

Thus the binomial probability in equation, can be written as

P(x₁, ≤ X ≤ x₂) = F(x₂)-(x₁)

∼ Φ (x₂ -np/√npq) - Φ (x₁-np/√npq)