Approximations to Poisson and Hgpergeometric Distributions:

Like the binomial probability, Poisson and the hypergeometric probabilities can be also approximated by the normal probability.

For a Poisson variable X having mean λ, the variance is λ. It can be proved that the cdf F ( x ) of Poisson distribution is approximated by Φ (x- λ/√λ)without the continuity correction and by Φ  ((x+1/2-λ)/√λ) using the continuity correction. Hence the Poisson probability

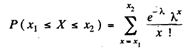
is approximated by

P(x1 ≤ X ≤ x2) ∼ Φ ((x2+1/2-λ)/√λ)-Φ ((x1-1/2 -λ)/√λ)

if continuity correction is used. Similar approximation holds for Hypergeometric distribution. The hypergeometric variable x has the pmf

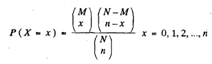
And

E(X) =nM/N =μ, say

V(X) = nM/N(1-M/N)(N-n/N-1) = σ², say

Hence the cdf F ( x ) is approximated with continuity correction by

 Φ ((x+1/2 -μ)/σ) and the hypergeometric probability

P(x1 ≤ X ≤ x2) =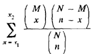 

∼ Φ ((x+1/2-μ)/σ) -Φ ((x-1/2-μ)/σ)