Mathematical definitions of NURBS curves:

The mathematical definitions of NURBS curves and surfaces are comparatively simple. A NURBS curve is a vector - valued piecewise rational polynomial function of the form.

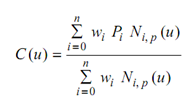                                                        ------------- (1)

Here w_i are the so-called weights, the P_i are the control points (just as in the case of non-rational curves), and N_{i, p} (u) are the normalized B-spline basis functions of degree p described recursively as

N_{i, p} (u)        = (u - u_i / u_{i + p -}   u_i) N_{i, p -1} (u) + (u_{i + p +1 -} u / u_{i + n +1 -} u _{i +1})  Ni +1, p -1 (u)                 -                                                                                    

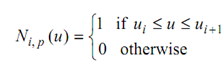                            ---------------(2)

Here u_i are the so-called knots forming a knot vector

U = (u₀ , u₁ , . . . , u_m )                                        ----------- (3)

The degree, number of knots, and number of control points are associated by the formula m = n + p + 1. For non-uniform & non-periodic B-splines, the knot vector takes the form

U = (α, α, . . . , u _{p +1}, . . . , u_{m - p -1}, β, β, . . . , β)                                 ------------- (4)

where the end knots ? and β are repeated along with multiplicity P + 1. In most of the practical applications ? = 0 and β = 0, as is supposed. The basis function Eq. (2) is explained over the entire line; though, the focus is on the interval [0, 1]. The NURBS CURVE (Eq. (1)) along with the knot vector (Eq. (4)) is a Bezier-like curve. It interpolates the endpoints and is tangential at the endpoints to the first and last legs of the control polygon. Most of the properties of non-rational curves apply to NURBS as well.

NURBS is capable of representing in a single form non-rational B-splines and Bezier curves, in addition to linear and quadric analytic curves, and may be utilized in approximating or interpolators mode. To illustrate the flexibility of the technique, Figure illustrated a number of NURBS curves of order 4 constructed by using the same point set, but with different weighting factors in the homogeneous coordinate system.