Mathematical definitions of NURBS:

The mathematical definitions of NURBS surfaces and curves are comparatively simple. A NURBS curve is a vector - appreciated piecewise rational polynomial function of the form.

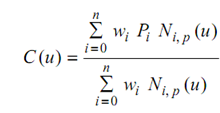                              ------------------ (1)

Here w_i are the so-called weights, the P_i are the control points (just as in the case of non-rational curves), & N_i, p (u) are the normalized B-spline basis functions of degree p described recursively as following

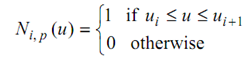
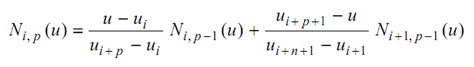--------(2)

here ui are the so-called knots forming a knot vector

U = (u₀ , u₁ , . . . , u_m )                               ------------- (3)

The number of knots, degree, and number of control points are connected by the formula m = n + p + 1. For and non-periodic and non-uniform B-splines, the knot vector provides the form

U = (α, α, . . . , u _{p +1}, . . . , u_{m - p -1}, β, β, . . . , β)                ------------- (4)

Here the end knots ? & β are repeated along multiplicity P + 1. In most of the practical applications ? = 0 & β = 0, as is supposed. The basis function Equation (2) is described over the whole line; but, the focus is on the interval [0, 1]. The NURBS CURVE (Eq. (1)) along the knot vector (Eq. (4)) is a Bezier-like curve. This interpolates the endpoints and is tangential at the endpoints to the primary and final legs of the control polygon. Mostly properties of non-rational curves apply to NURBS as well.

NURBS is able of representing in a single form non-rational Bezier curves and B-splines, along with quadric and linear analytic curves, and might be used in approximating or interpolators mode. To illustrate the flexibility of the technique, Figure 15 illustrated a number of NURBS curves of order 4 constructed utilizing the similar point set, but with several weighting factors in the homogeneous coordinate system.