Analytic and Geometric Properties:

The curve from Eq. (1) may be rewritten in the following equivalent form :

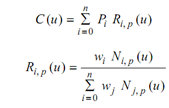
where R_{i, p} (u) are rational basis functions. Their analytic properties find out the geometric behaviour of curves. The most of the significant properties are :

•          Generalization: If all the weights are set to 1, then

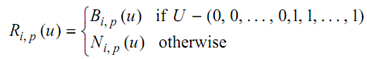
where the 0s and 1s in U are repeated along with multiplicity p + 1, and B_{i, p} (u) mention the Bernstein polynomials degree.

•          Locality:  R_{i, p} (u) = 0 if u ∉ [u_i , u_{i + p +1} ] .

•          Partition of Unity: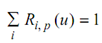       

•          Differentiability: In the interior of a knot span, the rational basis functions are infinitely continuously differentiable if the denominator is bounded away from zero. At a knot they are p-k times continuously differentiable whereas k is the multiplicity of the knot.

R_{i, p} (u; w_i  = 0) = 0

R_{i, p} (u; w_i  →+ ∞) = 1

R_{i, p} (u; w _j  → + ∞) = 0  j ≠ i