Resultant of Non-Coplanar Forces:

In particular case of non-coplanar force system also, the method of resolution of forces may be utilized to determine the resultant. If three non-coplanar forces F₁, F₂ & F₃ are acting at a point O in body, the resultant R₁₂ of the two forces F₁ & F₂ may be determined by law of parallelogram of forces. The force R₁₂ may next be combined with F₃ via the parallelogram, giving the resultant of three forces F₁, F₂ and F₃ as R. If all of there are more forces in the system, the similar process may be continued until all the forces have been covered. Here, note down that the resultant of non-coplanar force system should pass through the point of concurrence.

The resultant of concurrent force system may also be determined as the vector addition of the forces of the system. The vector sum of the forces may be obtained very easily if each force is resolved into rectangular components. Therefore, the vector sum of a non-coplanar system of concurrent forces F₁, F₂ & F₃ is

                                          R¯ = F¯₁ + F¯₂  + F¯₃

That may be written in rectangular component form as following :

R_x i¯ + R _y  j¯ + R_z k¯ = F_1x i + F_{1 y}  j¯ + F_1z k¯ + F_{2 x} i¯ + F_{2 y}  j¯ + F_{2 z} k¯ + F_{3 x} i¯ + F_{3 y}  j¯ + F_{3 z} k¯

= (F_1x  + F_{2 x}  + F_{3 x} ) i¯ + ( F_{1 y}  + F_{2 y}  + F_{3 y} ) j¯ + ( F_1z  + F_{2 z}  + F_{3 z} ) k¯

Thus,

= (∑ F_x ) i¯ + (∑ F_y ) j¯ + (∑ F_z ) k¯

R_x = F_1x + F_{2 x +} F_{3 x =} (∑ F_x)

R_y = F_1y + F_{2 y +} F_{3 y =} (∑ F_y)

R_z = F_1z + F_{2 z +} F_{3 z =} (∑ F_z)

At last, combining these components R_x, R_y and R_z vectorially, we obtain the resultant R¯ .

Therefore,

R¯ = R¯x i¯ + R¯y  j¯ + R¯z k¯

and

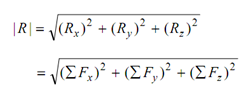
cos θ_x = ∑ F_x/ R , cos θ=∑ F_y/ R  , cos θ_z= ∑ F_z /R

Where θ_x, θ_y and θ_z are the angles which the resultant R makes with x, y and z axes, respectively.